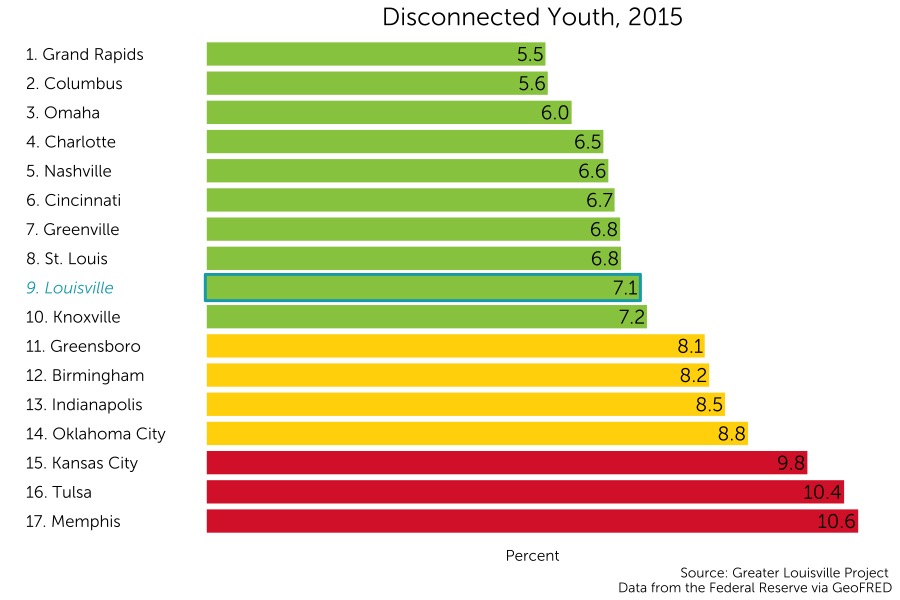
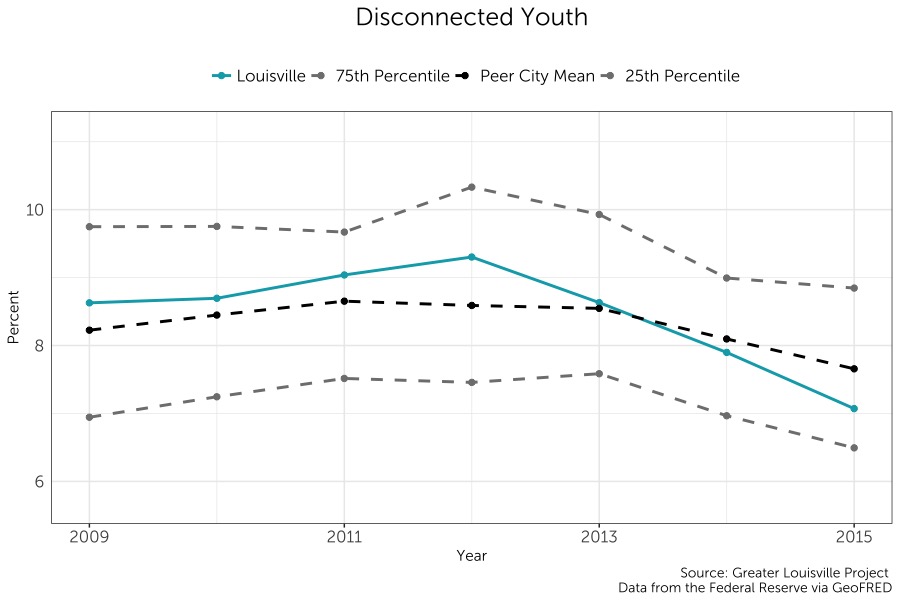
Disconnected Youth
The number of disconnected youth in a community is a good indicator of how that community is preparing its youth for a transition to adulthood. Disconnected youth often are not able to build their toolkit of skills for employment and often do not have the adequate social capital to fall back on in crisis situations. Because of these trends, disconnected youth are at a higher risk of experiencing homelessness or participating in criminal activity.